
論理回路 ブール代数を使って論理回路の問題を解く方法 ゆっくり Youtube
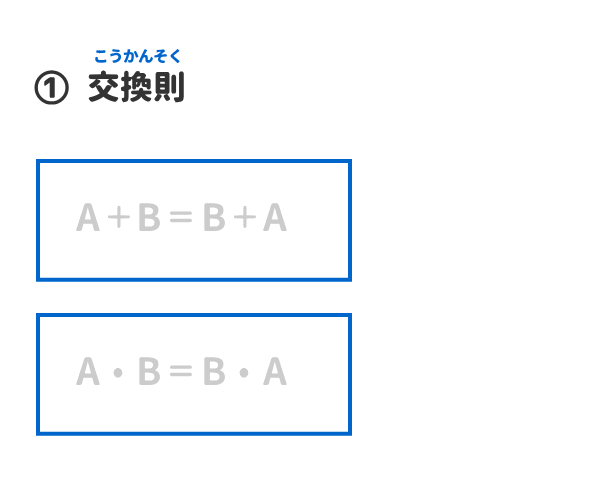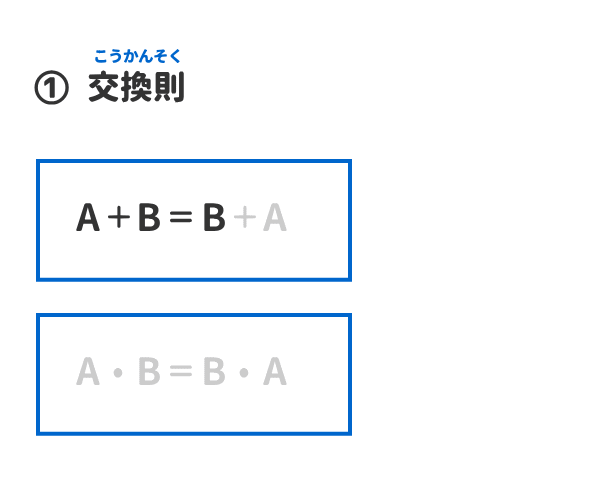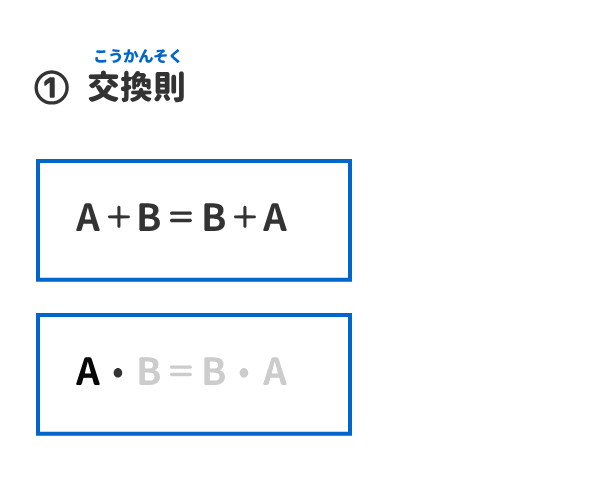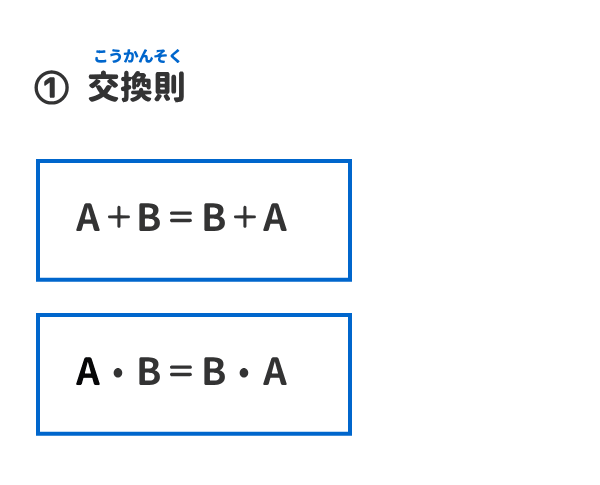
A B = B A A B = B A A ⋅ B = B ⋅A A ⋅ B = B ⋅ A 結合則 A (B C) = (A B) C A ( B C) = ( A B) C A ⋅ (B ⋅ C) = (A ⋅B) ⋅ C A ⋅ ( B ⋅ C) = ( A ⋅ B) ⋅ C 分配則 A(B C) = AB AC A ( B C) = A B A C A BC = (A B)(A C) A B C = ( A B) ( A C) 恒等則 を計算すると、 A= (A+B) (A+C) (B'+C'+D) = (A+AB+AC+BC) (B'+C'+D) = (A+BC) (B'+C'+D) =AB'+AC'+AD+BCD B= (A+D) (B+D) (A'+B'+C) = (AB+AD+BD+D) (A'+B'+C) = (AB+D) (A'+B'+C) =ABC+A'D+B'D+CD C= (A+C+D) (B'+D') (A+B) = (A+C+D) (AB'+AD'+BD') =AB'+AD'+ABD'+AB'C+ACD'+BCD'+AB'D =AB'+AD'+BCD'
ブール代数 解き方
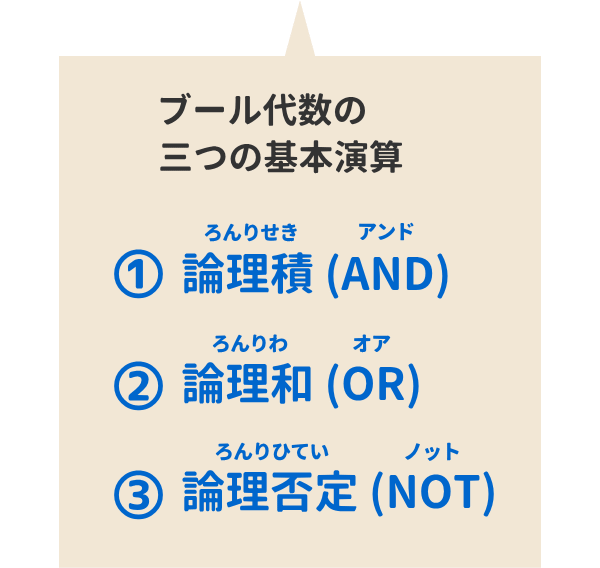
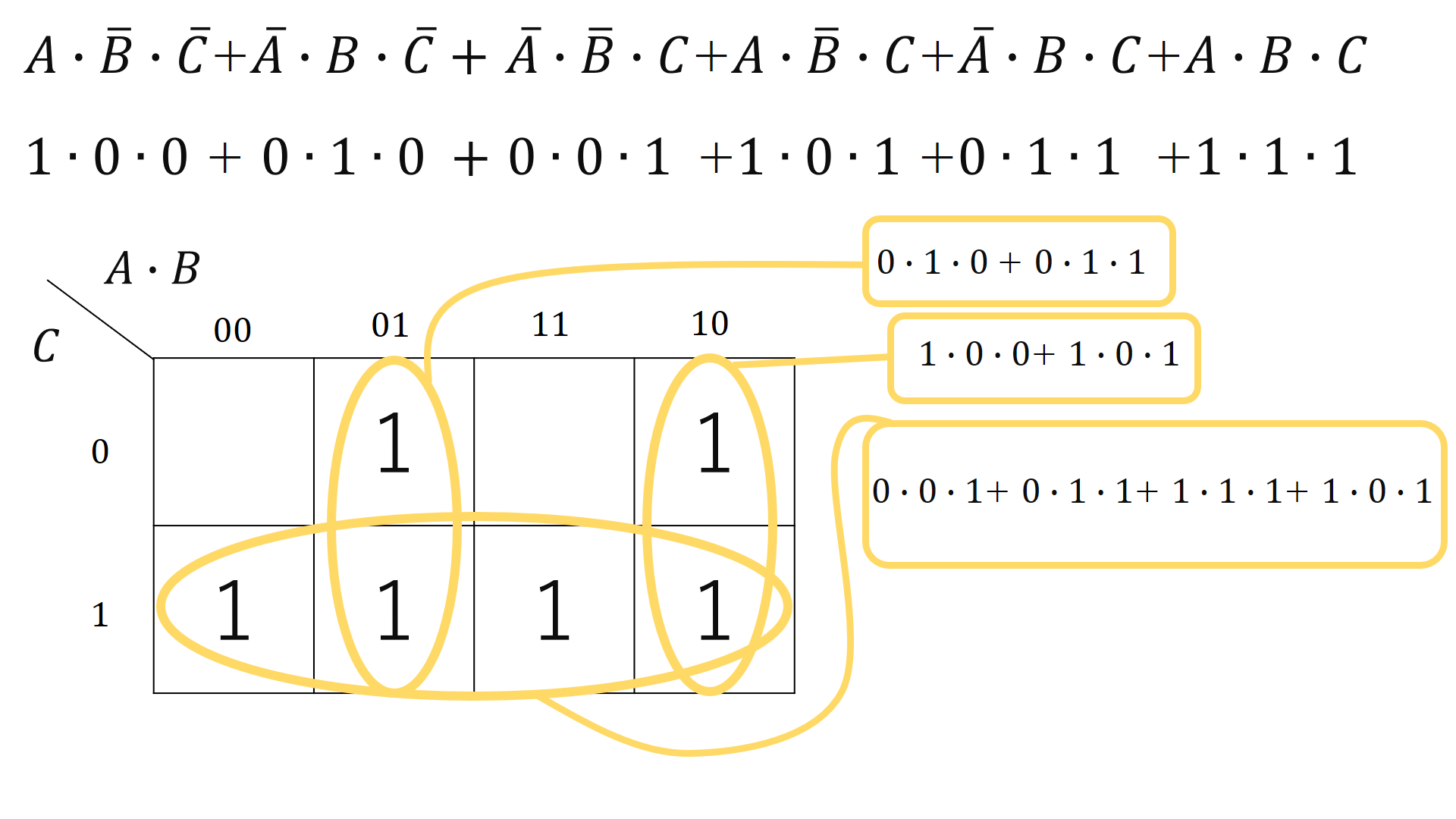
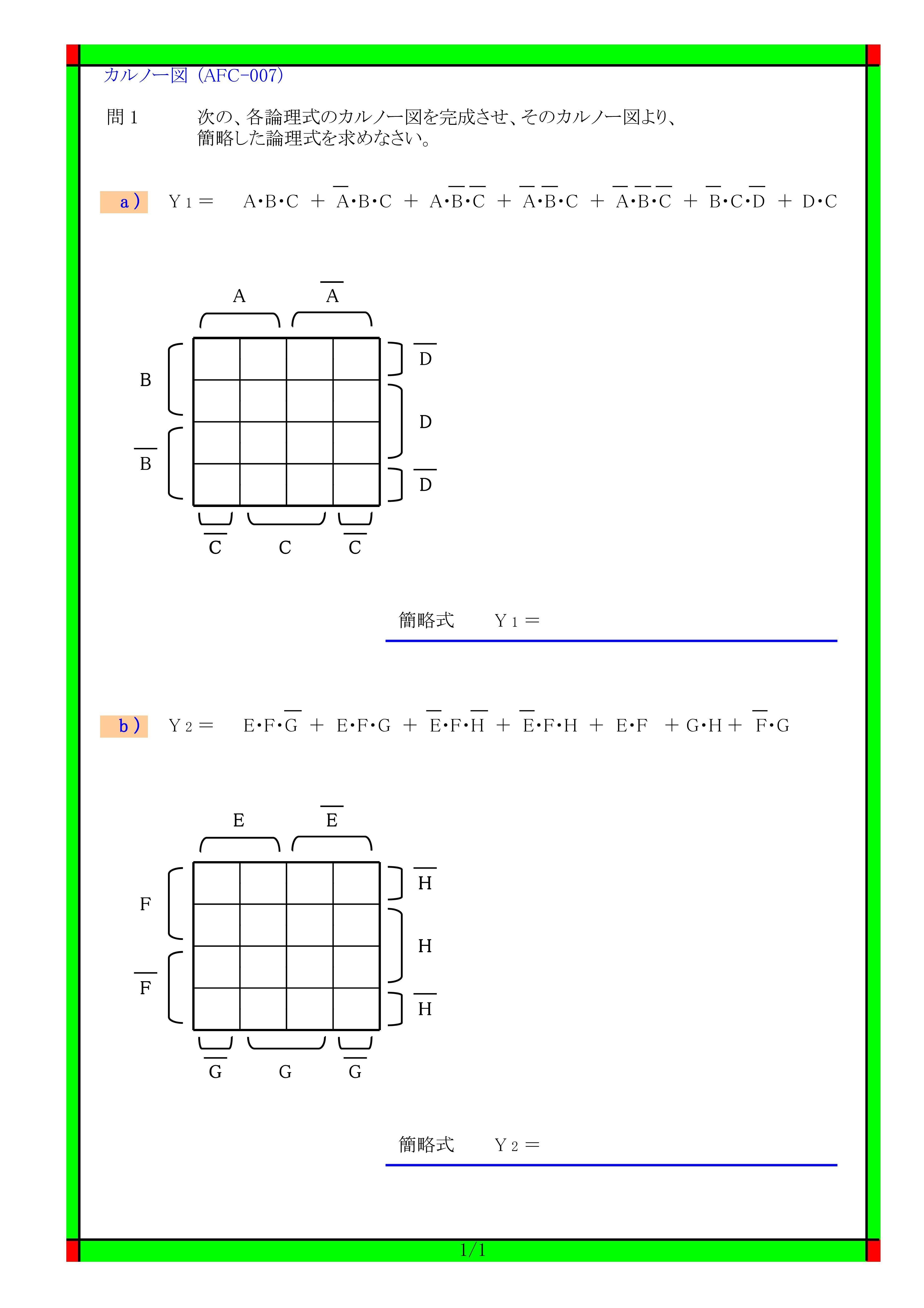
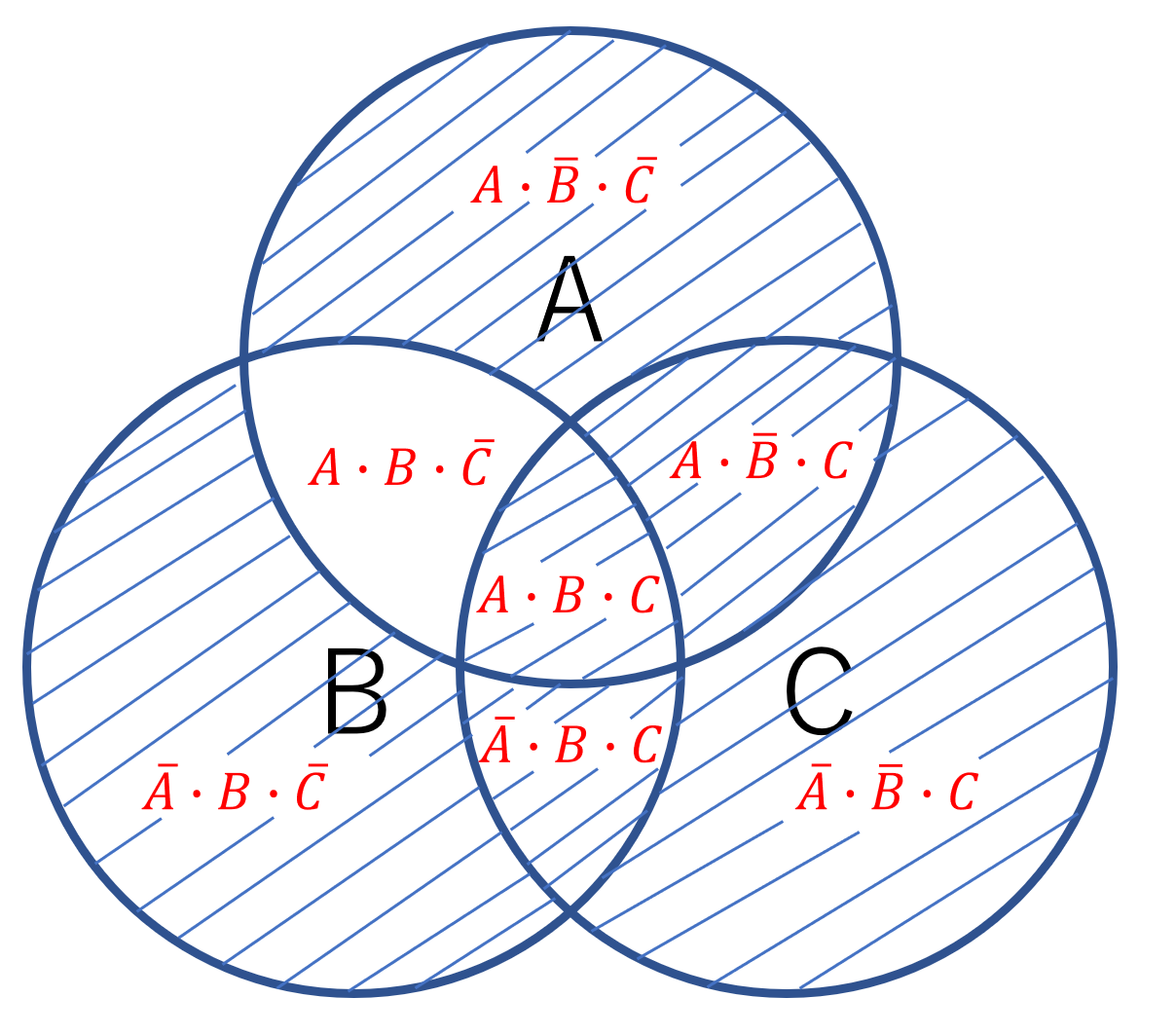
ブール代数 解き方-(1)ブール代数の公式を使う方法 (2)カルノー図を使う方法 (3)禁止項を利用する方法 1 カルノー図を利用する方法 カルノー図とは:平面図上に規則的に全ての最小項を表示した図. 論理式の簡単化を視覚的に行うときに使う図. ベン図とカルノー図の対比3変数の場合 a⋅b⋅c a⋅b ⋅c a⋅b ブール代数の簡略化の問題について教えてほしいです。 解決済 気になる やり方だけ説明します。 こつさえつかめば簡単です。
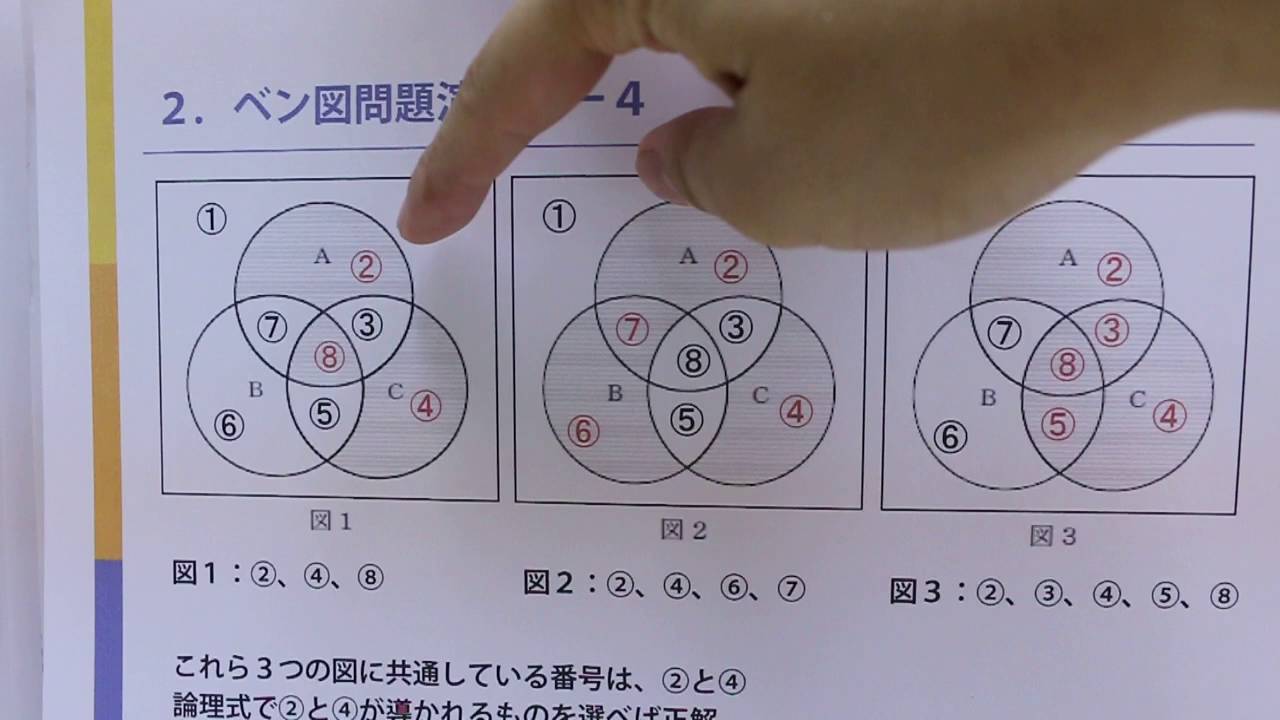
工事担任者 ベン図2 重要回 問題演習1 Youtube
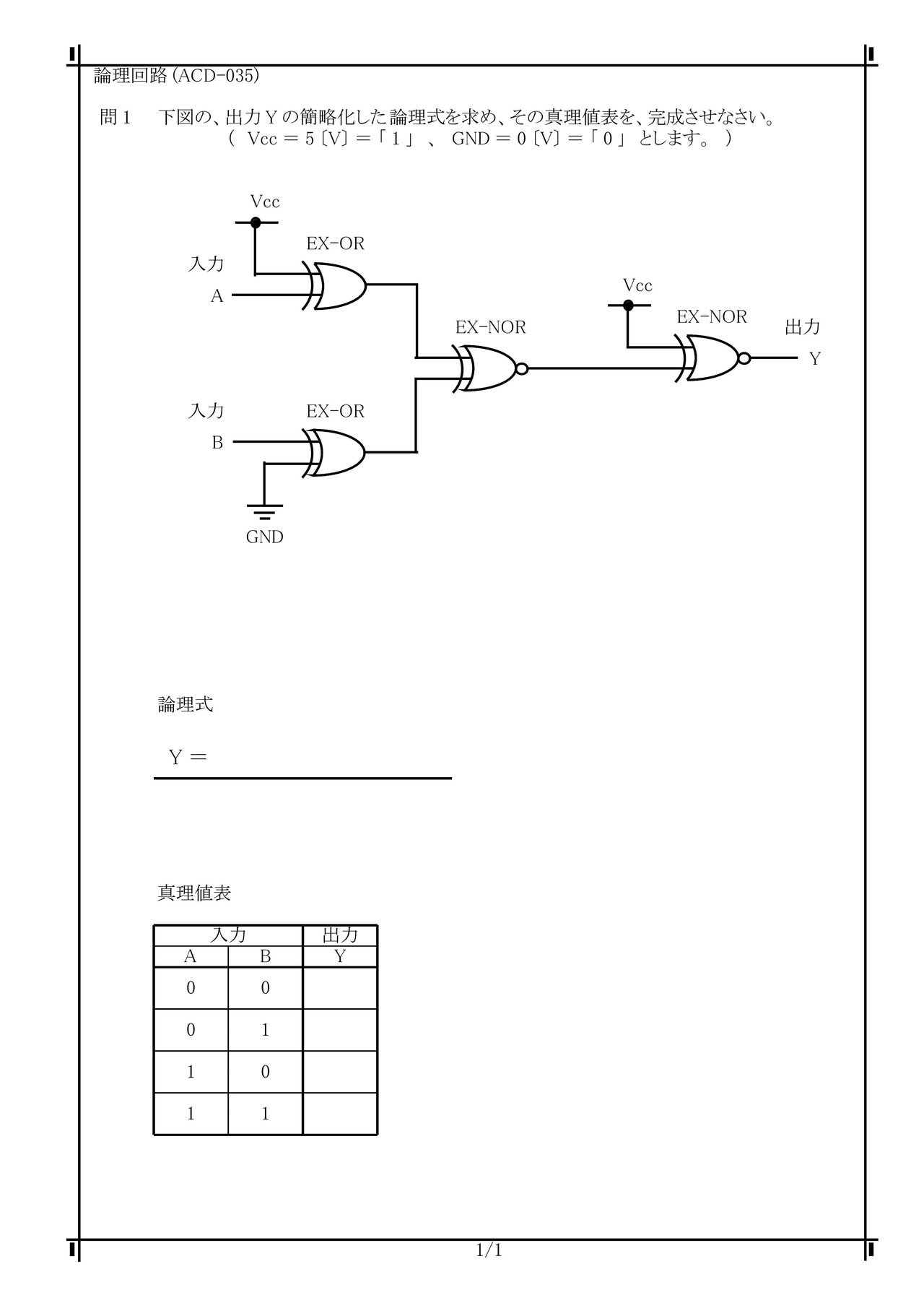
A¢b = b ¢a (1) 分配法則 a¢(b c) = (a¢b)(a¢c);基礎3 論理演算・ベン図、論理回路、フリップフロップ、ブール代数 ベン図の見方、論理演算、論理記号、 フリップフロップ回路の性質、ブール代数の演算(ドモルガン等)、二進数の足し算 基礎4 デシベル、ノイズ 計算問題 デシベル計算 対数計算ブール代数が出来なくても、暗記問題だけで十分合格点は狙えます! 論理演算の公式 本問1問に10分もかかるようなら、解かない方がマシです。 まずは他の問題を解き終えてから、残された時間で取り組むようにしましょう。 基礎;
A¢1 = a (3) 補元 aa¯ = 1; ブール代数ではこの0と1を二進数の数字として扱うのではなく、「真 (TRUE):1」と「偽 (FALSE):0」の二値だけを扱うのがブール代数です。 具体的に見ていきましょう。 通常の二進数として扱う場合、11=10となります。 一方で、ブール代数では11=10ではありません。 ブール代数では11=1となります。 ブール代数では0と1のみで桁を繰上りません。 そして A(¯¯¯¯A B) = AB A ( A ¯ B) = A B A ¯¯¯¯AB = A B A A ¯ B = A B 基本パターン3 AB ¯¯¯¯AC BC = AB ¯¯¯¯AC A B A ¯ C B C = A B A ¯ C (A B)(¯¯¯¯A C)(B C) = (A B)(¯¯¯¯A C) ( A B) ( A ¯ C) ( B C) = ( A B) ( A ¯ C) 上記式の証明や、論理式簡単化の練習問題は ブール代数論理式の簡単化 (解き方)のコツ練習問題付き
ブール代数 解き方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 | ||
「ブール代数 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
「ブール代数 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 | ||
「ブール代数 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
「ブール代数 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
「ブール代数 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 | ||
「ブール代数 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  | |
「ブール代数 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「ブール代数 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「ブール代数 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「ブール代数 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「ブール代数 解き方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |
排他的論理和の演算では結合則が成立するのでブール微分の順番には関係なく微分結果が得られる。 そこで次のように簡略化した表記法をとる。 (21) この表記法により3次微分は次のようになる。 (22) ブール微分の記法を使えば式(14)は、次のように表記できる。 (23) (24) 次へガロア標準形演算上へ特別講義2 資料5戻る3変数ガロア標準形 論理式を変形する手段として、「 ブール代数 4次の行列式の解き方を簡単に解説! 線形代数基底・次元とは? フーリエ変換例題集なんとなく学ぶフーリエ解析 行列の簡約化のやり方&コツを分かりやすく解説! 留数とは?求め方も分かりやすく解説!なんとなくわかる複素解





0 件のコメント:
コメントを投稿